mean

ythagorean means[edit]

Main article: Pythagorean means

Arithmetic mean (AM)[edit]

Main article: Arithmetic mean

The arithmetic mean (or simply "mean") of a sample ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$, usually denoted by ${\displaystyle {\bar {x}}}$, is the sum of the sampled values divided by the number of items in the sample:

${\displaystyle {\bar {x}}={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}$

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is

${\displaystyle {\frac {4+36+45+50+75}{5}}={\frac {210}{5}}=42.}$

Geometric mean (GM)[edit]

The geometric mean is an average that is useful for sets of positive numbers that are interpreted according to their product and not their sum (as is the case with the arithmetic mean) e.g. rates of growth.

${\displaystyle {\bar {x}}=\left(\prod _{i=1}^{n}{x_{i}}\right)^{\tfrac {1}{n}}}$

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:

${\displaystyle (4\times 36\times 45\times 50\times 75)^{^{1}/_{5}}={\sqrt[{5}]{24\;300\;000}}=30.}$

Harmonic mean (HM)[edit]

The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, for example speed (distance per unit of time).

${\displaystyle {\bar {x}}=n\cdot \left(\sum _{i=1}^{n}{\frac {1}{x_{i}}}\right)^{-1}}$

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is

${\displaystyle {\frac {5}{{\tfrac {1}{4}}+{\tfrac {1}{36}}+{\tfrac {1}{45}}+{\tfrac {1}{50}}+{\tfrac {1}{75}}}}={\frac {5}{\;{\tfrac {1}{3}}\;}}=15.}$

Relationship between AM, GM, and HM[edit]

Main article: Inequality of arithmetic and geometric means

AM, GM, and HM satisfy these inequalities:

${\displaystyle AM\geq GM\geq HM\,}$

Equality holds if and only if all the elements of the given sample are equal.

Statistical location[edit]

See also: Average § Statistical location

Comparison of the arithmetic mean, median and mode of two skewed (log-normal) distributions.

Geometric visualisation of the mode, median and mean of an arbitrary probability density function.^[5]

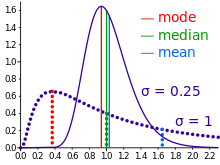
In descriptive statistics, the mean may be confused with the median, mode or mid-range, as any of these may be called an "average" (more formally, a measure of central tendency). The mean of a set of observations is the arithmetic average of the values; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely value (mode). For example, mean income is typically skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income, and favors the larger number of people with lower incomes. While the median and mode are often more intuitive measures for such skewed data, many skewed distributions are in fact best described by their mean, including the exponential and Poisson distributions.

Mean of a probability distribution[edit]

Main article: Expected value

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. In this context, it is also known as the expected value. For a discrete probability distribution, the mean is given by ${\displaystyle \textstyle \sum xP(x)}$, where the sum is taken over all possible values of the random variable and ${\displaystyle P(x)}$ is the probability mass function. For a continuous distribution,the mean is ${\displaystyle \textstyle \int _{-\infty }^{\infty }xf(x)\,dx}$, where ${\displaystyle f(x)}$ is the probability density function. In all cases, including those in which the distribution is neither discrete nor continuous, the mean is the Lebesgue integral of the random variable with respect to its probability measure. The mean need not exist or be finite; for some probability distributions the mean is infinite (+∞ or −∞), while others have no mean.

Generalized means[edit]

Power mean[edit]

The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric and harmonic means. It is defined for a set of n positive numbers x_i by

${\displaystyle {\bar {x}}(m)=\left({\frac {1}{n}}\cdot \sum _{i=1}^{n}{x_{i}^{m}}\right)^{\tfrac {1}{m}}}$

By choosing different values for the parameter m, the following types of means are obtained:

${\displaystyle m\rightarrow \infty }$	maximum of ${\displaystyle x_{i}}$
${\displaystyle m=2}$	quadratic mean
${\displaystyle m=1}$	arithmetic mean
${\displaystyle m\rightarrow 0}$	geometric mean
${\displaystyle m=-1}$	harmonic mean
${\displaystyle m\rightarrow -\infty }$	minimum of ${\displaystyle x_{i}}$

ƒ-mean[edit]

This can be generalized further as the generalized f-mean

${\displaystyle {\bar {x}}=f^{-1}\left({{\frac {1}{n}}\cdot \sum _{i=1}^{n}{f(x_{i})}}\right)}$

and again a suitable choice of an invertible ƒ will give

${\displaystyle f(x)=x}$	arithmetic mean,
${\displaystyle f(x)={\frac {1}{x}}}$	harmonic mean,
${\displaystyle f(x)=x^{m}}$	power mean,
${\displaystyle f(x)=\ln x}$	geometric mean.

Weighted arithmetic mean[edit]

The weighted arithmetic mean (or weighted average) is used if one wants to combine average values from samples of the same population with different sample sizes:

${\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}{w_{i}\cdot x_{i}}}{\sum _{i=1}^{n}{w_{i}}}}.}$

The weights ${\displaystyle w_{i}}$ represent the sizes of the different samples. In other applications they represent a measure for the reliability of the influence upon the mean by the respective values.

Truncated mean[edit]

Sometimes a set of numbers might contain outliers, i.e., data values which are much lower or much higher than the others. Often, outliers are erroneous data caused by artifacts. In this case, one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end, and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of total number of values.

Interquartile mean[edit]

The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.

${\displaystyle {\bar {x}}={2 \over n}\sum _{i=(n/4)+1}^{3n/4}{x_{i}}}$

assuming the values have been ordered, so is simply a specific example of a weighted mean for a specific set of weights.

Mean of a function[edit]

Main article: Mean of a function

In some circumstances mathematicians may calculate a mean of an infinite (even an uncountable) set of values. This can happen when calculating the mean value ${\displaystyle y_{\text{ave}}}$ of a function ${\displaystyle f(x)}$. Intuitively this can be thought of as calculating the area under a section of a curve and then dividing by the length of that section. This can be done crudely by counting squares on graph paper or more precisely by integration. The integration formula is written as:

${\displaystyle y_{\text{ave}}(a,b)={\frac {\int \limits _{a}^{b}\!f(x)\,dx\,}{b-a}}}$

• Tweet
• Share
• Share
• Share
• Share

About Admin MC3

This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.

Related Post